Dynamische Datenstrukturen
Wie alle Seiten auf diesem Server (bzw. meinem Teil davon) erhebt diese Seite keinen Anspruch auf Vollständigkeit. Darüberhinaus aber behauptet sie nicht einmal, auch nur einen Überblick über das Gebiet der dynamischen Datenstrukturen zu bieten. Sie dient lediglich dazu, die in anderen Programmen auf anderen Seiten verwendeten Strukturen verständlich darzustellen.
Es geht hier auch nicht darum, wie man unter Pascal Speicher alloziert und Pointer benutzt. Das ist Teil der Sprache Pascal bzw. sogar des entsprechenden Compilers1.
Verkettete Listen
Die verkettete Liste (oder auch linked list) ist eine der grundlegenden dynamischen Datenstrukturen. Das Prinzip besteht darin, daß jeder gespeicherte Datensatz einen Zeiger auf seinen Nachfolger enthält. Angenommen, man wolle Zahlen in einer Liste speichern, dann könnte die Datenstruktur beispielsweise so aussehen:
type PList = ^TList; TList = record Num : Integer; Next : PList; end;
Der einzelne Datensatz kann also nicht nur Auskunft über die gespeicherte Zahl geben, sondern auch darüber, wo der Rest der Liste zu finden ist. Die Darstellung im Speicher sieht dann also so aus:

Man kann eine Liste auch als rekursive Datenstruktur betrachten: Sie besteht aus einem Kopf und einem Zeiger auf die Restliste (auch "Head" und "Tail" genannt). Diese besteht wiederum aus einem Kopf und einem Zeiger auf die Restliste usw, bis allerdings die Restliste gleich nil ist.
In Pascal definiert man zwei Funktionen, die diese Werte zurückgeben:
function Head(List : PList) : Integer; begin Head := List^.Num; end; function Tail(List : PList) : PList; begin Tail := List^.Next; end;
Damit kann man jetzt die Liste von vorn nach hinten durchgehen, z. B. um ein Element zu suchen, oder um irgendetwas anderes mit den Elementen zu machen. Ein Spezialfall davon ist das Abbilden (engl. mapping), das eine Funktion auf jedes Element der Liste anwendet, und die Ergebnisse in einer zweiten Liste ablegt.
Um Listen zusammenzusetzen, gibt es zwei grundsätzliche Möglichkeiten: Man kann
von einem einzelnen Element ausgehen, und es vor eine bestehende Liste hängen
(dabei kann diese auch nil sein); oder man kann zwei Listen
konkatenieren (d. h. zusammenhängen). Die erste Funktion wird
naheliegenderweise so geschrieben:
procedure Cons(Elem : Integer; var List : PList); var NewList : PList; begin New(NewList); NewList^.Num := Elem; NewList^.Next := List; List := NewList; end;
Das neue Element wird zunächst mit New erzeugt, und anschließend
wird sein Next auf den alten Anfang der Liste gesetzt. Zum
Abschluß wird es selbst als die neue Liste zurückgegeben. Die Konkatenation
könnte beispielsweise so aussehen:
procedure Concat(List1 : PList; List2 : PList); begin if List1 = nil then exit; while List1^.Next <> nil do List1 := List1^.Next; List1^.Next := List2; end;
Wie man sieht, wird List1 zunächst bis zum letzten Element durchgegangen
– welches daran zu erkennen ist, daß sein Next-Zeiger
nil ist – und dann wird List2 einfach daran angehängt. Die
Prozedur könnte natürlich auch davon Gebrauch machen, daß die Liste eine
rekursive Datenstruktur ist; man erhält dann eine rekursive Prozedur, die
aber ganz ähnlich funktioniert.
Die Unit linkedlist.pas stellt einen Typen TList zur Verfügung, der allerdings keine Zahlen speichert, sondern Pointer. Auf diese Weise ist er universell verwendbar und nicht auf einen bestimmten Einsatzzweck festgelegt. Eine kurze Demo wird in dem Programm lite.pas gegeben.
Queue
Die Queue, zu deutsch Warteschlange, ist ein sog. FIFO-Speicher. FIFO steht für "First in, first out", was soviel besagt, als daß die Datensätze in der gleichen Reihenfolge ausgelesen werden, wie sie gespeichert worden sind. Die folgende Abbildung zeigt das Schema der Warteschlange:

Am linken Ende werden neue Elemente hinzugefügt, am rechten Ende werden
Elemente entnommen. Dazu bieten Queues normalerweise die beiden
Grundoperationen Enqueue und Dequeue zum Hinzufügen
und Entfernen von Elementen. Ein Prädikat IsEmpty kann
darüberhinaus feststellen, ob die Schlange leer ist.
Die Implementation erfolgt als verkettete Liste. Aus Effizienzgründen ist es dabei üblich, neben einem Zeiger auf den Anfang der Liste auch stets einen auf das Ende der Liste bereitzuhalten. Die beiden Grundoperationen können dann ganz einfach implementiert werden:
Enqueue hängt ein Element ans Ende der Liste an, und aktualisiert
den End-Zeiger entsprechend. Dequeue setzt den Anfangs-Zeiger auf
den Nachfolger des ersten Element und gibt dieses zurück.
Die Unit queue.pas stellt eine solche Queue als abstrakten Datentyp zur Verfügung. Zu beachten ist, daß der Zeiger auf das letzte Element hier "Tail" genannt wird - dies ist nicht zu verwechseln mit dem Tail-Begriff in Bezug auf verkettete Listen! Ein Programm, das Gebrauch von dieser Unit macht, ist der Bucketsort für Strings. Seine Funktionsweise wird auf der Suchen-und-Sortieren-Seite beschrieben.
Stack
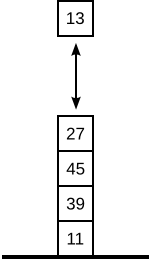
Im Gegensatz zur Queue ist der Stack (engl. stack = Haufen, Stapel) eine
LIFO-Datenstruktur (Last in, first out). Die Elemente werden also in der
umgekehrten Reihenfolge entnommen. Man kann sich den Stack als einen Stapel
vorstellen, auf den man nur oben etwas herauflegen, und von dem man nur von
oben etwas herunternehmen kann. Die Operationen zum Hinzufügen und Entnehmen,
hier Push und Pop genannt, operieren also nur auf dem
obersten Element:
(Im Deutschen wird der Stack auch häufig Kellerspeicher genannt. Welche
Vorstellungen von einem Keller dem zugrunde liegen, ist mir allerdings unklar
- wer seine Lebensmittelvorräte so behandelt, wird bald ein Problem haben...)
Die Implementation als verkettete Liste ist ebenso einfach wie naheliegend:
Für Push, das Hinzufügen eines Elementes, wird ein neues
Listenelement erzeugt und vorne an die Liste angehängt. Beim Poppen eines
Elementes wird es genauso einfach wieder weggenommen.
Stets zur Hand hat man den Stack mit der Unit stack.pas.
Bäume
Häufig sollen Daten hierarchisch gepeichert werden. Dies bedeutet, daß ein Datensatz "Oberelement" von mehreren "Unterelementen" ist; man spricht auch von Vater und Kindern. Diese können wiederum Väter von mehreren Unterelementen sein usw. Weil die Struktur immer weiter verästelt, wird sie auch Baum genannt:
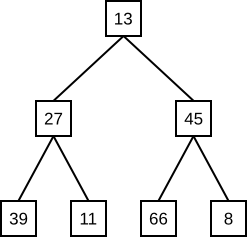
Das oberste Element (die Elemente in Bäumen heißen übrigens Knoten, weil Bäume Graphen sind) ist die Wurzel, die Elemente in der untersten Reihe stellen die Blätter dar. Der abgebildete Baum zeichnet sich außerdem dadurch aus, daß jeder Knoten genau zwei Nachfolger hat - es handelt sich um einen binären Baum.
Man kann sich den Baum ähnlich wie eine verkettete Liste vorstellen, nur daß jedes Element nicht nur einen, sondern mehrere Nachfolger hat. Ist die Anzahl der Nachfolger fest, ist daher die Implementation recht einfach, wie z. B. im Falle eines binären Baums für Zahlen:
type PBinTree = ^TBinTree; TBinTree = record Num : Integer; Left : PBinTree; Right : PBinTree; end;
(Die Namen Left und Right sind natürlich beliebig,
genausogut könnten sie Up und Down oder
Charme und Strange heißen.) Auch, bzw. gerade Bäume
sind natürlich rekursive Datenstrukturen; um Bäume zu durchsuchen, sind
rekursive Algorithmen häufig die naheliegendste Lösung. Wie erwähnt,
werden Bäume normalerweise eingesetzt, um Daten hierarchisch zu speichern. Ein
bekanntes Beispiel sind hierarchische Dateisysteme - unter Windows NT bspw.
kann man sich mit dem Befehl tree die Verzeichnisse als Baum
anzeigen lassen. Unter Unix-Systemen zeigt pstree die
Prozeßhierarchie an.
Das Programm fulldir.pas ist ein schönes Beispiel für das rekursive Durchsuchen des Verzeichnisbaums. Es zeigt alle Dateien in einem Verzeichnis an, inklusive aller Dateien in den Unterverzeichnissen, die natürlich auch wieder Unterverzeichnisse haben können usw... Das Programm ist leicht zu modifizieren, um z. B. die Datei checksum.ms aus allen Unterverzeichnissen zu löschen.
Statische Versionen
Schlangen, Stacks und Bäume können auch mit statischem Speicher verwirklicht werden. Was zunächst mal nicht besonders naheliegend klingt, macht in manchen Fällen durchaus Sinn. Ein bekanntes Beispiel, das jeder kennt (auch wenn er sich dessen vielleicht nicht unbedingt bewußt ist), ist der Tastaturpuffer, der in jedem PC vorhanden ist. Eine klassische Warteschlange: Der Tastatur-Treiber speist Daten ein, die Programme lesen sie aus. Der Puffer ist üblicherweise 32 Byte groß; ist er voll, piepst der PC herum. Ein anderes Beispiel ist der Heapsort-Algorithmus, der auf der Suchen-und-Sortieren-Seite beschrieben ist, und der einen binären Baum in einem Array speichert.
Der Nachteil einer statischen Repräsentation liegt klarerweise darin, daß der Speicherplatz feststeht und die Struktur nicht wachsen kann. Auf der anderen Seite steht die einfache und ausgesprochen effiziente Implementierung. Davon abgesehen wäre es gelinde gesagt ungewöhnlich, in einer BIOS-Routine Speicher allozieren zu wollen.
Die statische Veriante des Stack ist die leichteste Übung. Die Elemente werden in einem Array gespeichert, und ein Index zeigt stets auf die momentane Spitze des Stacks. Beispiel:
34 65 99 01 12 00 00 00
^
Push(23);
34 65 99 01 12 23 00 00
^
Die maximale Größe des Stack ist hier 8, alle weiteren Push-Operationen müssen
abgelehnt werden. Es gilt: IsEmpty := Index = 0;
Die Warteschlange ist etwas komplizierter, dafür aber auch direkt aus der
dynamischen Version ableitbar. Wir haben einen Zeiger auf den Anfang und einen
auf das Ende? Kein Problem, führen wir zwei Indizes ein! Die Indizes heißen
in (wo ein neues Element geschrieben werden kann) und
out (wo das nächste gelesen werden kann). Zu beachten ist, daß
diese Indizes "überrollen", d. h. wenn sie über das Ende
hinauswandern, geht es am Anfang weiter. Ist in = out, so ist die
Schlange leer; ist in = out - 1, so ist die Schlange voll.
Beispiel:
00 00 00 68 24 09 78 00
o i
Enqueue(27); Enqueue(56); Dequeue;
56 00 00 68 24 09 78 27
i o
Das Überrollen kann man dabei ganz einfach realisieren, indem man den Array null-basiert macht, und dann einfach modulo mit der Array-Größre rechnet. Enqueue beispielsweise wird dann also so realisiert:
procedure Enqueue(z : LongInt); begin Queue[i] := z; i := (i + 1) mod QueueSize; end;
Eine Möglichkeit, Bäume statisch zu speichern, ist auf der oben erwähnten Seite über Such- und Sortieralgorithmen detailliert beschrieben.
Eine Kopie aus dem Pascal User Manual von Jensen und Wirth:
